Creating prompt chains to implement self-consistency prompting and least-to-most prompting

Step-by-step examples and free templates

Today’s post is going to be a little bit different. Rather than go deep into a single recent research paper, we’ll focus on two prompt engineering methods and ways to implement them.

The two methods we’ll look at are:

1. Self-consistency

2. Least-to-most prompting

For each of these methods, we’ll run through a few examples.

For the more visual inclined, this video covers the implementation portion of least-to-most prompting:

Self-Consistency Prompting

Self-consistency prompting is when you run a prompt many times and have the model select the most consistent answer, rather than just running the prompt once and going with the initial answer.

Below is an example of the flow.

The original research paper can be found here

As you can see, the prompt is run three times. Twice the output is $18, and once it is $26. Since $18 was the most consistent, that becomes the final answer.

You could use a rules-based approach in code for this type of example, or you could use an LLM with a prompt like:

I have generated the following responses to the question: {{ question }}
Responses:
1. {{response_1}}
2. {{response_2}}
3. {{response_3}}
Based on the above responses, select the most consistent answer.

We have a prompt template in PromptHub for this as well (you can access it here):

Access the template in PromptHub here

What makes this prompting method so great is how flexible it is. You can change what you want the LLM to optimize for by swapping out “consistent” for whatever word you’d like.

Implementing Self-Consistency Prompting

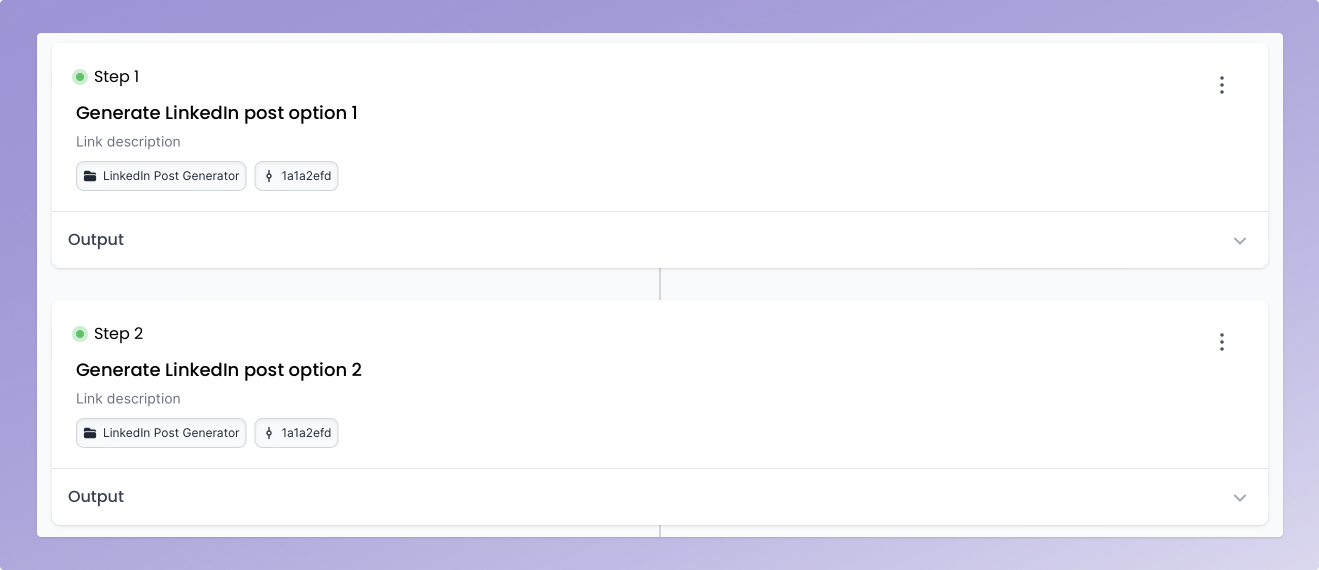
Let’s say we want to generate LinkedIn posts based on articles from the PromptHub blog.

We’ll implement self consistency prompting in three steps:

1. Write a prompt to generate the LinkedIn posts

2. Generate multiple LinkedIn posts

3. Leverage the self-consistency prompt template to pick the most exciting post

Step 1: Write a prompt to generate the LinkedIn posts

First step is write a quick prompt to generate LinkedIn posts based on articles:

Create a LinkedIn short post to help promote our most recent blog post.

Make sure it is written in our tone: {{Tone}}.

Here is the article to create the LinkedIn post about:

"""

{{content}}

"""

Here is a examples of what a post might be:

Example 1:

"""

{{ Example_Linkedin_Post }}

"""

Step 2: Generate multiple LinkedIn posts

Next up, we’ll need to run the prompt multiple times. We’ll use PromptHub’s prompt chaining feature to run the prompt three times.

Step 3: Leverage the self-consistency prompt template to pick the most exciting post

For the last prompt in our chain, we’ll use the self consistency prompt template above with to select the most exciting output.

I have generated the following responses to the question: {{ question }}
Responses:
1. {{response_1}}
2. {{response_2}}
3. {{response_3}}
Based on the above responses, select the most exciting answer.

We’ll pass the outputs from the previous steps into the {{response}} variables.

And just like that, we’re done. Additionally, we can run this anytime a new blog post is published just by tweaking the {{content}} variable in our LinkedIn post generator prompt.

What I like most about this setup is:

1. More options: Rather than just taking what the LLM gives you, this method allows for three separate options (perhaps generated with varying temperatures) to be considered.

2. Automated selection: No need to eyeball it myself if I trust in the LLM to make a good decision here. If I were worried about the LLM’s decision-making process, I could pass along a few-shot example of three posts and what I deem as the most exciting one.

Least-to-most prompting

Next up is least-to-most prompting. Least-to-most is a prompting method that enhances reasoning via two steps:

1. Break down problems into multiple subproblems

2. Sequentially solve subproblems

It is similar to chain-of-thought in that it prompts the model to perform explicit reasoning. But least-to-most prompting is a little more structured in its approach.

Below is an example of the flow.

The original research paper can be found here:

What I really like about this method is that you can easily apply it to a wide variety of problems. Also, it’s easy to understand, as it mimics how we solve problems. Breaking down problems into smaller subproblems is what we humans are great at.

Implementing least-to-most prompting

Before implementing this method, let’s look at an example prompt for each step.

Here is an example of a prompt used for the decomposition step. It has a single example of how to break down a similar question, and then leaves the model to fill in the decomposition steps for answering the next question.

Decomposition prompt

Q: It takes Jake 3 minutes to stack a tower of cups. It takes him 2 minutes to unstack them. The activity session ends in 20 minutes. How many times can he stack and unstack the cups before the session ends?

A: To solve the problem "How many times can Jake stack and unstack the cups before the session ends?", we need to:

1. Determine the total time it takes for one complete cycle (stack + unstack).

2. Calculate how many complete cycles he can do within the available time of 20 minutes.

Q: It takes Emma 4 minutes to climb a ladder. It takes her 1 minute to climb down. The park closes in 15 minutes. How many times can she climb the ladder before it closes?

A:

Let’s say the output is something like:

Decomposition output

To solve the problem "How many times can Emma climb the ladder before the park closes?", we need to:

1. **Determine the total time it takes for one complete cycle** (climbing up + climbing down).

2. **Calculate how many complete cycles she can do within the available time of 15 minutes**.

Next up is the prompt to start solving the subproblems. You could either have the model solve each subproblem independently or all at once. This decision depends on your preference and the complexity of your use case.

Since this is a relatively easy problem, we’ll just use a single prompt.

Sequential solving prompt

Solve the following subproblems in order to answer the question: "How many times can Emma climb the ladder before the park closes?"

1. **Determine the total time it takes for one complete cycle** (climbing up + climbing down).

2. **Calculate how many complete cycles she can do within the available time of 15 minutes**.

The output would be something like:

Sequential solving output

Determine the total time it takes for one complete cycle (climbing up + climbing down).

-Emma takes 4 minutes to climb up and 1 minute to climb down, so each cycle takes 4+1=54+1=5 minutes.

Calculate how many complete cycles she can do within the available time of 15 minutes.

-Divide the total available time by the time for one cycle: 15 minutes5 minutes/cycle=3 cycles5 minutes/cycle15 minutes​=3 cycles.

Therefore, Emma can climb the ladder 3 times before the park closes.

Great, now let’s move on to solving a more real-world use case.

Let’s create a system flexible enough to solve any type of problem, not just ones related to a specific task.

To do this, we’ll use three prompts:

1. Generate few-shot examples of problems being broken down into subproblems; this will show the model how to decompose similar problems.

2. Decompose the problem at hand into subproblems, using the few-shot examples from the previous prompt to guide the model.

3. Solve the subproblems.

Step 1: Generate few-shot examples

Below is the template we’ll use to generate few-shot examples, for any type of problem:

Your job is to generate few-shot examples for the following task: {{ task }}

Your few-shot examples should contain two parts: A problem, and the decomposed subproblems. It should follow the structure below:

"""

Problem: Problem description

Decomposed subproblems:

- Subproblem 1

- Subproblem 2

- Subproblem 3

"""

Your output should contain only the examples, no preamble

This will allow us to input any value into the {{task}} variable, making this very flexible.

Access the template in PromptHub here

Step 2: Decompose the task into subproblems

Now that we have a few examples of similar problems being decomposed, we’ll want to move on to generating the subproblems for the specific task at hand.

We’ll pass along the task we want to be decomposed, as well as the output from the previous step, which will help "show" the model how to decompose similar tasks.

{{ task }}

List only the decomposed subproblems that must be solved before solving the task listed above. Your output should contain only the decomposed subproblems, no preamble

Here are a few examples of problems and their respective decomposed subproblems: {{ few-shot-examples}}

Access the template in PromptHub here

Step 3: Solve the task!

Now that we have a list of subproblems for our task, it’s time to get to solving them!

Solve the following task by addressing the subproblems listed below.

Task: {{ task }}

Subproblems: {{sub-problems}}

Access the prompt in PromptHub here

Great! Now we have three individual prompts that we can use to implement Least-to-Most Prompting for any task.

But wouldn’t it be better if we could chain them together and automate the process of passing the output from one prompt as the input for another? Wouldn’t it be extra awesome if we could do this without writing any code? With PromptHub’s prompt chains, we can!

All we need to do is pass the few-shot examples from the first step to the second prompt, and then pass the subproblems generated in the second prompt to the final prompt.

And we’re done! We now have a prompt chain that we can use to leverage Least-to-Most Prompting for any task.

Conclusion

This one was a lot of fun. Seeing how prompt methods can be translated easily into real-world examples is always a blast. If you have any questions about implementing either of these methods, just reply to this email or reach out directly.

Happy prompting!

Dan